Geordnetes Paar: Definition von Frege

aus GlossarWiki, der Glossar-Datenbank der Fachhochschule Augsburg

Dieser Artikel erfüllt die GlossarWiki-Qualitätsanforderungen:

Korrektheit: 4
(großteils überprüft) 		Umfang: 4
(unwichtige Fakten fehlen) 		Quellenangaben: 5
(vollständig vorhanden) 		Quellenarten: 5
(ausgezeichnet) 		Konformität: 5
(ausgezeichnet)

Der Artikel „Geordnetes Paar“ befasst sich mit der Geschichte und den wichtigsten Definitionen des „geordneten Paares“. Die älteste mir bekannte Definition, die den Paar-Begriff auf zuvor definierte Grundbegriffe zurückführt, ist die Definition von Gottlob Frege.

Da die Symbolik, die Frege verwendet, ungewöhnlich ist (dies war einer der Gründe, warum er zu Lebzeiten wenig Anerkennung fand[1]), ist seine Definition nicht ohne Weiters zu verstehen. Im Folgenden soll daher versucht werden, diese Definition etwas zu veranschaulichen.

Frege (1893)[2]

Definition des geordneten Paars, Frege (1893), §144, S. 179[2]

Wir definiren nun das Paar so:

$ \Vdash\acute{\epsilon}(o \frown (a \frown \epsilon)) = o; a $

Das Semikolon ist hierbei zweiseitiges Functionszeichen. (Frege (1893), §144, S. 179[2])

Probleme mit dem Verständnis von Freges Definition

Freges Definition ist nicht zu verstehen, wenn man seine Symbolik nicht kennt oder falsch interpretiert. Zum Beispiel merkt Richard Heck zu dieser Definition fälschlicherweise an, dass sie weder mengentheoretisch noch mit Hilfe der Prädikatenlogik zweiter Ordnung konsistent nachgebildet werden kann:

Unfortunately, Frege's definition of ordered pairs is, as George Boolos once put it, extravagant and can not be consistently reconstructed, either in second-order logic or in set-theory.[3]

Auch ist nicht notwendigerweise jeder Versuch, diese Definition in eine moderne Form zu zu bringen, von Erfolg gekrönt. Der C.S. Peirce Professor of American Philosophy Randall Dipert übersetzt Freges Definition beispielsweise folgendermaßen:

$ <x,y> := \{x,\{y\}\} $[4]

Er merkt an, dass diese Definition falsch ist, weil z.B. die Paare $ <\{\{c\}\}, c> $ und $ <\{c\}, \{c\}> $ nicht unterschieden werden könnten, da sie beide durch $ \{\{\{c\}\}, \{c\}\} $ repräsentiert würden. Das stimmt zwar, ist aber nicht Freges Definition anzulasten, sondern Diperts falscher Interpretation dieser Definition.

Gottlob Frege definiert das Paar $ o;a $ mit Hilfe eines „Werthverlaufs“ $ \acute{\epsilon}\phi(\epsilon) $ und der „Function $ \xi \frown \zeta $ mit zwei Argumenten“ (Frege (1893, §9 und §34)[2]). Da Frege der Funktion $ \frown $ keinen Namen gibt, soll diese im Folgenden „Frown“ heißen (in Anlehnung an den Namen des LaTeX-Symbols, mit dem sie in diesem Beitrag dargestellt wird).

Um die Definition von Frege zu verstehen, muss man die Bedeutung des Wertverlaufs einer Funktion und die Frown-Funktion kennen. Auch hier leitet die Literatur einen leicht in die Irre. Beispielsweise interpretiert Edward Zalta (2014, Abschnitt 2.3) die Frown-Operation als Element-Operation $ \in $.[5] Das ist richtig, falls der Wertverlauf einer Prädikatsfunktion betrachtet wird, d.h. einer Funktion, die jedes Element des Frege-Universums auf einen Wahheitswert abbildet. Eine derartige Funktion wird von Frege „Begriff“ genannt (Zalta verwendet die englische Übersetzung “concept”). Die Frown-Funktion von Frege ist allerdings nicht nur für Wertverläufe von „Begriffen“ definiert, sondern für Wertverläufe von beliebigen Funktionen. Das heißt, i. Allg. kann man $ \frown $ nicht mit $ \in $ gleichsetzen.

Wertverlauf und Frown-Funktion

Freges Definition

$ \Vdash\acute{\epsilon}(o \frown (a \frown \epsilon)) = o;a $

enthält drei unübliche Symbole, deren Bedeutungen im Folgenden näher beleuchtet werden: $ \Vdash $, $ \acute\cdot $ und $ \frown $.

Der Definitionsdoppelstrich

$ \Vdash $ ist der „Definitionsdoppelstrich“, der von Frege als Erweiterung des „Urtheilstrichs“ $ \vdash $ definiert wird (Frege (1893, §27 und §5)[2]). Das Symbol $ \vdash $ wird in der Logik heute noch als „Herleitungs“-, „Ableitungs“- oder „Inferenzoperator“ verwendet.

Der Definitionsdoppelstrich sagt zusammen mit dem Gleichheitszeichen $ = $ aus, dass der Term $ o;a $ eine abkürzende Schreibweise für den Term $ \acute{\epsilon}(o \frown (a \frown \epsilon)) $ ist. Heutzutage würde man üblicherweise folgende Schreibweise verwenden:

$ o;a := \acute{\epsilon}(o \frown (a \frown \epsilon)) $

Der Wertverlaufsoperator

Der Operator $ \acute\cdot $ wird von Frege genutzt, um den „Werthverlauf“ einer Funktion zu beschreiben (Frege (1893), §9[2]). Laut Kutschera (1989, S. 96)[6] kann man den Wertverlauf $ \acute{\epsilon}\phi(\epsilon) $ einer Funktion $ \phi $ in heutigen Klassensystemen durch die Klasse $ \{[\epsilon,\phi(\epsilon)]: \top\} $ ausdrücken, wobei die Objekte $ [x,y] $ keine Frege-Paare sind, sondern geordnete Paare des zugrundeliegende Klassensystems (Wiener-/Kuratowski-/Quine-/Morse-/Schmidt-Paare o. Ä.; siehe Artikel „geordnetes Paar“).

Für Frege sind Funktionen allerdings grundlegender als Klassen. In seinem Axiomensstem sind Funktionen (und deren Wertverläufe) wie beim Lambda-Kalkül von Alonzo Church Grundbegriffe, die nicht definiert, sondern nur erläutert werden können[6] und mit deren Hilfe andere Gundbegriffe wie Klassen, Paare, natürliche Zahlen etc. definiert werden.

Denselben Weg schlägt beispielsweise auch John von Neumann (1925) ein.[7] Allerdings unterscheidet sich sein Axiomensystem hinsichtlich der Definition des geordneten Paares in zwei wesentlichen Punkten von Freges Axiomensystem:

  • Es erlaubt nicht die uneingeschränkte Bildung von Funktionen und geordneten Paaren, so dass die Russellsche Antinomie mit großer Wahrscheinlichkeit, aber – aufgrund des zweiten Gödelschen Unvollständigkeitssatzes – nicht beweisbar vermieden wird.
  • Geordnete Paare werden axiomatisch eingeführt und nicht per Definition.

Überlicherweise werden heute allerdings meist mengen- oder klassenbasierte Systeme (wie z.B. Zermelo-Fraenkel-Mengenlehre, Neumann-Bernays-Gödel-Mengenlehre, Quine-Rosser-Mengenlehre) zur Formalisierung der Mathematik eingesetzt. In diesen Systemen wird zwischen einer Funktion und ihrem Wertverlauf i. Allg. nicht mehr unterschieden. Im Gegenteil: Funktionen werden mit Hilfe von Wertverlaufsklassen definiert (siehe z.B. Schmidt (1966)[8]): Eine Funktion $ f $ ist eine Klasse von Paaren, wobei es keine zwei Paare $ [x, y_1], [x, y_2] \in f $ gibt, für die $ y_1 \not= y_2 $ gilt.

Da Funktionen (genauer: Wertverläufe von Funktionen) wesentlich für die Definition des Freges-Paares sind, können Funktionen nicht mit Hilfe des Frege-Paares definiert werden. Dies war aber auch nicht die Absicht von Frege. Er benötigte die Paare zur Konstruktion von reellen Zahlen (vgl. Frege (1903, §161 ff.)[9], Kutschera (1989, S. 125)[6]).

Um sich Frege-Paare zu veranschaulichen, kann man dennoch einen Trick anwenden: Man identifiziert Funktionen mit ihrem Wertverlauf (so wie das in Klassensystemen üblich ist). Das einzige Problem, das man sich dabei einhandelt, ist, dass Frege-Paare $ a;b $ dann – sofern man eine moderne klassenbasierten Theorie zu Hilfe nimmt – mit Hilfe von anderen Paaren $ [a,b] $ definiert werden. Das ist aber nichts Ungewöhnliches. So werden z.B. auch Morse-Paare[10] mit Hilfe von Kuratowski-Paaren[11] definiert.

Alternativ kann man sich den Wertverlauf-Operator als Lambda-Operator vorstellen (vgl. Zalta (2014)[5]):

$ \acute{\epsilon}\phi(\epsilon) \;\hat=\; \lambda \epsilon .\phi(\epsilon) $

Wenn man die η-Konversion im Lambda-Kalkül zulässt, sieht man auch hier, dass der Wertverlauf von $ \phi $ mit $ \phi $ selbst identifiziert werden kann:

$ \lambda \epsilon .\phi(\epsilon) \;=\; \phi $

Frege betrachtet nicht nur arithmetische Funktionen, sondern auch Prädikatsfunktionen. Diese heißen bei ihm „Begriffe“ (Frege (1893, §3, S. 8)[2]). Eine Pädikatsfunktion liefert für alle Argumente einen Wahrheitswert T oder F als Ergebnis. Frege bezeichnet diese Werte als „das Wahre“ und „das Falsche“. Wenn $ \phi $ eine Prädikatsfunktion ist, die jedem Objekt im Frege-Universum einen Wahrheitswert zuordnet, kann der Wertverlauf von $ \phi $ auch als Klasse aufgefasst werden, die alle Elemente (Frege: „Gegenstände“) $ \epsilon $ enthält, für die $ \phi(\epsilon) $ wahr ist. Der Wertvelauf $ \acute{\epsilon}\phi(\epsilon) $ entspricht unter dieser Sichtweise der Klasse $ \{\epsilon: \phi(\epsilon)\} $ (vgl. Kutschera (1989, Kapitel 6.4)[6]). Insbesondere definiert Frege die leere Menge und einelementige Mengen mit Hilfe von Wertverläufen (führt dafür aber keine eigenen Symbole ein):

moderne Definition Freges Definition Quellen
leere Menge $ \emptyset := \{x: x\not=x\} $ $ \acute{\epsilon}\neg(\epsilon=\epsilon) $ Klasse, Frege (1893, S. 53, vorletzter Absatz)[2]
Einermenge $ \{a\} := \{x: x=a\} $ oder
$ \{a\} := \{x: \rm{Mg}(a) \rightarrow x = a\} $		 $ \acute{\epsilon}(\epsilon=a) $ Klasse, Frege (1893, §11)[2]
Extraktion des Elements
einer Einermenge		 Es sei $ a $ eine Menge.
$ A =\{a\} \rightarrow \bigcup{A} = a $		 Wenn $ A =\acute{\epsilon}(\epsilon=a) $, dann $ \backslash A = a $

Schmidt (1966, S72, 8.28)[8], Frege (1893, §11)[2]

Für alle Objekte $ A $, die keine Einermenge sind, setzt Frege fest, dass $ \backslash A = A $ gilt. Das heißt, für die leere Menge liefern $ \bigcup $ und $ \backslash $ ebenfalls dasselbe Ergebnis (nämlich die leere Menge). Für alle anderen Objekte $ A $ unterscheiden sich die Ergebnisse von $ \bigcup A $ und $ \backslash A $ dagegen. Dies ist für die Veranschaulichung der Frown-Funktion, die im nachfolgenden Abschnitt beschrieben wird, jedoch nicht von Belang, da bei der Definition dieser Funktion nur die leere Menge und einelementige Mengen benötigt werden.

Definition der Frown-Funktion, Frege (1893, §34, S. 53)[2]

Die Frown-Funktion

Frege definiert die Frown-Funktion folgendermaßen (Frege (1893, §34, S. 53)[2]):

$ \Vdash\backslash\acute{\alpha}(\neg\bigwedge g : u = \acute{\epsilon}g(\epsilon) \rightarrow \neg (g(a) = \alpha)) = a \frown u $

Dies kann man mit Hilfe der Operatoren $ \bigvee $ und $ \wedge $ (die Frege allerdings nicht explizit definiert und daher auch nicht explitizt verwendet) etwas einfacher ausdrücken, da $ \neg \bigwedge g: a \rightarrow \neg b $ äquivalent zu $ \bigvee g: a \wedge b $ ist:

$ \Vdash\backslash\acute{\alpha}(\bigvee g : u = \acute{\epsilon}g(\epsilon) \wedge g(a) = \alpha) = a \frown u $

In einem modernen Klassensystem kann man diese Definition – da es sich bei $ \bigvee g : \ldots $ um eine Prädikatsfunktion handelt und es höchstens ein Element $ \alpha $ gibt, das dieses Prädikat erfüllt, da also $ \backslash A $ und $ \bigcup A $ dasselbe Ergebnis liefern – folgendermaßen formulieren:

$ a \frown u := \bigcup\{\alpha : \bigvee g : u = \acute{\epsilon}g(\epsilon) \wedge g(a) = \alpha\} $

(der Wertlauf $ \acute{\epsilon}g(\epsilon) $ repräsentiert hier natürlich die Klasse $ \{[\epsilon,y]: y=g(\epsilon)\} $)

Zwei Fälle sind zu unterscheiden: Entweder ist $ u $ der Wertverlauf einer Funktion g oder $ u $ ist dies nicht. Im ersten Fall gilt:

$ \vdash a \frown \acute{\epsilon}g(\epsilon) = \bigcup\{\alpha : g(a) = \alpha\} = g(a) $

Frege beweist auf den Seiten 74 und 75 denselben Satz in folgender Form:

$ \vdash f(a) = a \frown \acute{\epsilon}f(\epsilon) $ (Dieser Satz erhält von Frege die Satznummer 1.)

Im zweiten Fall gilt:

$ \vdash a \frown u = \bigcup\{\alpha : \bigvee g : u = \acute{\epsilon}g(\epsilon) \wedge g(a) = \alpha\} = \bigcup\{\alpha : \bot\} = \emptyset $

$ a \frown u $ liefert also, falls u der Wertverlauf einer Funktion $ g $ ist, den Wert der Funktion $ g $ für das Argument $ a $ als Ergebnis. Falls $ u $ kein Wertverlauf ist, hat $ a \frown u $ dagegen die leere Menge als Ergebnis. (vgl. Frege (1893, S. 53, letzter Absatz)[2]; Kutschera (1989, S. 104)[6]).

Im Falle einer Prädikatsfunktion entspricht der $ \frown $-Operator dem in Klassensystem üblichen Elementoperator $ \in $:

$ a \frown \acute{\epsilon}g(\epsilon) = g(a) $ entspricht in diesem Fall folgender Beziehung $ a \in \{\epsilon: g(\epsilon)\} \leftrightarrow g(a) $

Dies ist der Spezialfall, mit dem sich Zalta näher befasst[5].

Satz 1 und Satz 2: Der Wertverlauf von ein- und zweistelligen Funktionen, Frege (1893), S. 75[2]

Frege zeigt auf S. 75 außerdem noch, dass sein Satz 1

$ \vdash f(a) = a \frown \acute{\epsilon}f(\epsilon) $

auch für zweistellige Funktionen verallgemeinert werden kann:

$ \vdash f(a,b) = a \frown (b \frown \acute{\alpha}\acute{\epsilon}f(\epsilon,\alpha)) $ (Dieser Satz erhält von Frege die Satznummer 2.)

Analog zu Frege kann man auch

$ \vdash f(a)(b) = a \frown (b \frown \acute{\alpha}\acute{\epsilon}f(\epsilon)(\alpha)) $

zeigen. Das heißt, $ f(a,b) $ und $ f(a)(b) $ unterscheiden sich im Prinzip nicht. Obwohl Frege diese alternative Notation für Funktionen mit zwei Argumenten nicht verwendet hat, wird dsie im nächsten Abschnitt zur Veranschaulichung der Paardefinition verwendet, um die Definitionen etwas schlanker zu halten.

Anmerkung: Auf dieselbe Weise könnte man auch den Wertverlauf von beliebigen n-stelligen Funktionen definieren. Dies hat Frege allerdings nicht getan.

„Übersetzung“ von Freges Definition in „moderne“ Symbolik

Aus den vorangegangenen Überlegungen folgt, dass man in modernen Klassensystemen Freges Paardefinition

$ \Vdash\acute{\epsilon}(o \frown (a \frown \epsilon)) = o; a $

mit Hilfe des Lambda-Kalküls (das dem Axiomensystem von Frege gerade hinsichtlich des Wertverlauf-Operators etwas näher steht als ein Klassensystem) folgendermaßen formulieren kann:

$ o;a \,:= \; \lambda \epsilon . \epsilon a o $

Für die „Übersetzung“ von Freges Definition in eine klassenbasierte Definition werden folgende Vereinbarungen getroffen.

  • Eine Funktion $ f $ ist eine Klasse von Paaren mit $ [x,y_1], [x,y_2]\in f \rightarrow y_1=y_2 $.
  • Der Funktionsaufruf-Operator $ \cdot(\cdot) $ ist folgendermaßen definiert $ f(x) := \bigcap\{y: [x,y] \in f \} $.

Damit definiert man:

$ o; a := \{ [\epsilon, \epsilon(a)(o)] : \top\} $, d.h, $ o; a $ ist eine Funktion mit $ (o; a)(\epsilon) = \epsilon(a)(o) $

Sofern $ \epsilon $ eine Funktion ist, für die der zweistellige Funktionsaufruf $ \epsilon(a)(o) $ definiert ist, stimmen Freges Definition und die Alternative-Definition überein. Für andere Funktionen und Nicht-Funktionen gilt dagegen bei Frege stets $ (o;a)(\epsilon) = \emptyset $. Dies ist bei der Alternativdefinition nicht der Fall. Allerdings ist es für die weiteren Betrachtungen nicht wichtig, welchen Wert $ (o;a)(\epsilon) $ annimmt, falls $ \epsilon(a)(o) $ nicht definiert ist.

Das Paaraxiom

Beweis des Paaraxioms, Teil 1, Frege (1893, S. 195)[2]
Beweis des Paaraxioms, Teil 2, Frege (1893, S. 185)[2]

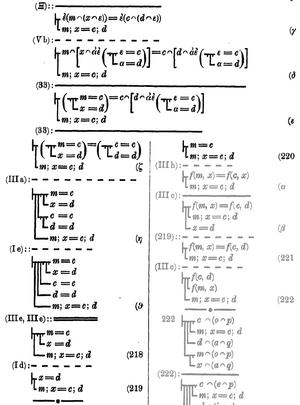
Frege beweist die Gültigkeit des Paaraxioms direkt, d. h. ohne Hilfe von Projektionsoperatoren und des Satzes „Aus der Existenz zweier Projektionsoperatoren für geordnete Paare folgt das Paaraxiom“:

TO BE DONE

Die Projektionsoperatoren

Frege gibt für seine Paardefinition keine Projektionsoperatoren an. Es ist aber kein Problem, diese zu definieren. Und damit ist ebenfalls sichergestellt, dass das Paaraxiom erfüllt ist.

Die Definition der Projektionsoperatoren kann in modernen Axiomensystemen auf (mindestens) zwei Arten erfolgen:

  1. Mit Funktionen eines Mengen- oder Klassensystems.
  2. Mit Hilfe des Lambda-Kalküls.

Man stellt fest, dass im zweiten Fall die Projektionsoperatoren wesentlich prägnanter formuliert werden können. Das liegt daran, dass es sich sowohl beim Lambda-Kalkül, als auch beim Axiomensystem von Frege um funktionale Axiomensysteme handelt.

Die Projektionsoperatoren auf Basis von Funktionen eines Mengen- oder Klassensystems

$ \begin{array}{lclclclclclcl} \rm{id} & := & \{[x,x] : \top \} & \rm{d.h.:} & \rm{id}(x) & = & x \\ \rm{const_c} & := & \{[x,c] : \top \} & \rm{d.h.:} & \rm{const_c}(x) & = & c \\ \pi'_1 & := & \{[x,\rm{id}] : \top \} & \rm{d.h.:} & \pi'_1(x) & = & \rm{id} \\ & & & \rm{d.h.:} & \pi'_1(x)(y) & = & \rm{id}(y) = y \\ \pi'_2 & := & \{[x,\rm{const}_x] : \top \} & \rm{d.h.:} & \pi'_2(x) & = & \rm{const}_x \\ & & & \rm{d.h.:} & \pi'_2(x)(y) & = & \rm{const}_x(y) = x \\ \pi_1 & := & \{ [p, p(\pi'_1)] : \top\} & \rm{d.h.:} & \pi_1(p) & = & p(\pi'_1) \\ \pi_2 & := & \{ [p, p(\pi'_2)] : \top\} & \rm{d.h.:} & \pi_2(p) & = & p(\pi'_2) \end{array} $

$ \pi_1 $ und $ \pi_2 $ sind die gesuchten Projektionsoperatoren:

$ \begin{array}{lcll} \pi_1(a;b) & = & (a;b) (\pi'_1) & (\rm{Def. von}\;\pi_1) \\ & = & \pi'_1(b)(a) & (\rm{Def. von}\;a;b) \\ & = & \rm{id}(a) & (\rm{Def. von}\;\pi'_1)\\ & = & a & (\rm{Def. von}\;\rm{id}) \\ \pi_2(a;b) & = & (a;b) (\pi'_2) & (\rm{Def. von}\;\pi_2) \\ & = & \pi'_2(b)(a) & (\rm{Def. von}\;a;b) \\ & = & \rm{const}_b(a)& (\rm{Def. von}\;\pi'_2)\\ & = & b & (\rm{Def. von}\;\rm{const}_b) \end{array} $

Die Projektionsoperatoren auf Basis des Lambda-Kalküls

$ \begin{array}{lclclcl} \pi_1 & := & \lambda p. p(\lambda x.\lambda y.y) \\ \pi_2 & := & \lambda p. p(\lambda x.\lambda y.x) \end{array} $

$ \pi_1 $ und $ \pi_2 $ sind die gesuchten Projektionsoperatoren:

$ \begin{array}{lcll} \pi_1(a;b) & = & (a;b) (\lambda x.\lambda y.y) & (\rm{Def. von}\;\pi_1) \\ & = & (\lambda \epsilon . \epsilon b a)(\lambda x. \lambda y. y) & (\rm{Def. von}\;a;b) \\ & = & (\lambda x. \lambda y. y) b a & (\rm{\beta{-}Konversion}) \\ & = & (\lambda y. y) a & (\rm{\beta{-}Konversion}) \\ & = & a & (\rm{\beta{-}Konversion}) \\ \pi_2(a;b) & = & (a;b) (\lambda x.\lambda y.x) & (\rm{Def. von}\;\pi_2) \\ & = & (\lambda \epsilon . \epsilon b a)(\lambda x. \lambda y. x) & (\rm{Def. von}\;a;b) \\ & = & (\lambda x. \lambda y. x) b a & (\rm{\beta{-}Konversion}) \\ & = & (\lambda y. b) a & (\rm{\beta{-}Konversion}) \\ & = & b & (\rm{\beta{-}Konversion}) \\ \end{array} $

„Rückübersetzung“ der Projektionsoperatoren in Freges Notation

Die Projektionsoperatoren des vorangegangenen Abschnitts können ziemlich einfach in Freges Notation übersetzt werden:

$ \begin{array}{lclclcl} \Vdash \acute{p}(p(\acute{x}(\acute{y}y))) = \pi_1 \\ \Vdash \acute{p}(p(\acute{x}(\acute{y}x))) = \pi_2 \\ \end{array} $

$ \pi_1 $ und $ \pi_2 $ sind die gesuchten Projektionsoperatoren. Der Beweis des Satzes basiert im Wesentlichen auf Satz 1 von Frege: $ \vdash f(a) = a \frown \acute{\epsilon}f(\epsilon) $ (§54, S. 75[2]).

$ \begin{array}{lcll} \vdash \pi_1(a;b) & = & \acute{p}(p(\acute{x}(\acute{y}y)))(a;b) & (\rm{Def. von}\;\pi_1) \\ & = & (a;b) \frown \acute{p}(p(\acute{x}(\acute{y}y))) & (\rm{Frege: Satz 1}) \\ & = & (a;b)(\acute{x}(\acute{y}y)) & (\rm{Frege: Satz 1}) \\ & = & \acute{x}(\acute{y}y) \frown (a;b) & (\rm{Frege: Satz 1}) \\ & = & \acute{x}(\acute{y}y) \frown (\acute{\epsilon}(a \frown (b \frown \epsilon)) & (\rm{Def. von}\;a;b) \\ & = & a \frown (b \frown \acute{x}(\acute{y}y)) & (\rm{Frege: Satz 1}) \\ & = & a \frown \acute{y}y & (\rm{Frege: Satz 1}) \\ & = & a & (\rm{Frege: Satz 1}) \\ \vdash \pi_2(a;b) & = & \acute{p}(p(\acute{x}(\acute{y}x)))(a;b) & (\rm{Def. von}\;\pi_2) \\ & = & (a;b) \frown \acute{p}(p(\acute{x}(\acute{y}x))) & (\rm{Frege: Satz 1}) \\ & = & (a;b)(\acute{x}(\acute{y}x)) & (\rm{Frege: Satz 1}) \\ & = & \acute{x}(\acute{y}x) \frown (a;b) & (\rm{Frege: Satz 1}) \\ & = & \acute{x}(\acute{y}x) \frown (\acute{\epsilon}(a \frown (b \frown \epsilon)) & (\rm{Def. von}\;a;b) \\ & = & a \frown (b \frown \acute{x}(\acute{y}x)) & (\rm{Frege: Satz 1}) \\ & = & a \frown \acute{y}b & (\rm{Frege: Satz 1}) \\ & = & b & (\rm{Frege: Satz 1}) \end{array} $

Frage-Paare als JavaScript-Funktionen

Da Fregepaare mit Hilfe von Funktionen definiert werden und JavaScript Funktionen als First-Class-Objekte behandelt, kann man Freges Definition sehr leicht mit Hilfe von JavaScript nachbilden: 

/* Diesen Code können Sie direkt in der JavaScript-Konsole Ihres Browser ausführen. */
let                              // λx.e  is expressed by  x => e
  pair = (o,a) => ε => ε(a)(o),  // o;a = λε.εao
  π1   = p => p(x => y => y),    // π1 = λp.p(λx.λy.y)
  π2   = p => p(x => y => x),    // π2 = λp.p(λx.λy.x),
  p    = pair(1111, 2222);

console.log( π1(ε => ε('one')('two')) ); // --> 'one'
console.log( π2(ε => ε('one')('two')) ); // --> 'two'

console.log( π1(p) ); // --> 1111
console.log( π2(p) ); // --> 2222

Source: EcmaScript6 (arrow functions), EcmaScript5

Wenn man bereits erzeugte Frege-Paare in einem Hasharray speichert und diese wiederverwendet, kann man sogar erzwingen, dass wertgleiche Paare im Sinne von JavaScript identisch (===) sind: 

console.log( pair('one','two') ===  pair('one','two'));  // --> true

Source: EcmaScript6 (arrow functions), EcmaScript5

Quellen

  1. ↑ Wußing (2009): Hans Wußing; 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise – Von Euler bis zur Gegenwart; Hrsg.: H.W. Alten, A. Djafari Naini und H. Wesenmüller-Kock; Band: Band 2; Auflage: 1; Verlag: Springer-Verlag GmbH; Adresse: Berlin; ISBN: 3642023630; 2009; Quellengüte: 5 (Buch), S. 402
  2. ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 2,13 2,14 2,15 2,16 Frege (1893): Gottlob Frege; Grundgesetze der Arithmetik; Band: I; Verlag: Verlag Hermann Pohle; Adresse: Jena; Web-Link 0, Web-Link 1, Web-Link 2, Web-Link 3; 1893; Quellengüte: 5 (Buch)
  3. ↑ Heck (1997): Richard G. Heck Jnr.; Definition by Induction in Frege's Grundgesetze der Arithmetik; in: Frege: Philosophy of Mathematics; Hrsg.: William Demopoulos; Verlag: Harvard University Press; Adresse: Cambridge; ISBN: 9780674319431; Web-Link 0, Web-Link 1; 1997; Quellengüte: 5 (Buchartikel)
  4. ↑ Dipert (1982): Randall R. Dipert; Set-Theoretical Representationsof Ordered Pairs and TheirAdequacy for the Logicof Relations; in: Canadian Journal of Philosophy; Band: XII; Nummer: 2; Seite(n): 353-374; Verlag: University of Calgary Press; Web-Link 0, Web-Link 1, Web-Link 2; 1945; Quellengüte: 5 (Artikel), S. 355
  5. ↑ 5,0 5,1 5,2 Zalta (2014): Edward N. Zalta; Frege's Theorem and Foundations for Arithmetic; Hrsg.: Edward N. Zalta; Reihe: The Stanford Encyclopedia of Philosophy; Band: 2014; Nummer: 4; Hochschule: Stanford University; http://plato.stanford.edu/entries/frege-theorem/index.html; Quellengüte: 5 (Web)
  6. ↑ 6,0 6,1 6,2 6,3 6,4 Kutschera (1989): Franz von Kutschera; Gottlob Frege – Eine Einfügrung in sein Werk; Verlag: Walter de Gruyter GmbH; Adresse: New York; Web-Link; 1989; Quellengüte: 5 (Buch)
  7. ↑ Neumann (1925): John von Neumann; Eine Axiomatisierung der Mengenlehre; in: Journal für die reine und angewandte Mathematik; Band: 154; Seite(n): 219-240; ISSN: 0075-4102, 1435-5345; Web-Link 0, Web-Link 1; 1925; Quellengüte: 5 (Artikel)
  8. ↑ 8,0 8,1 Schmidt (1966): Jürgen Schmidt; Mengenlehre – Grundbegriffe; Reihe: B.I.Hochschultaschenbücher; Band: 1; Nummer: 56; Verlag: Bibliographisches Institut AG; Adresse: Mannheim; ISBN: B0000BUJC6; 1966; Quellengüte: 5 (Buch)
  9. ↑ Frege (1903): Gottlob Frege; Grundgesetze der Arithmetik; Band: II; Verlag: Verlag Hermann Pohle; Adresse: Jena; Web-Link 0, Web-Link 1; 1903; Quellengüte: 5 (Buch)
  10. ↑ Morse (1965): Anthony Perry Morse; A Theory of Sets; Reihe: Pure and Applied Mathematics; Band: 18; Verlag: Academic Press; Adresse: New York, London; Web-Link; 1965; Quellengüte: 5 (Buch)
  11. ↑ Kuratowski (1921): Kazimierez Kuratowski; Sur la notion de l‘ordere dans la Théorie des Ensembles; in: Fundamenta Mathematica; Band: 2; Nummer: 1; Seite(n): 161-171; Web-Link; 1921; Quellengüte: 5 (Artikel)
Abgerufen von „https://glossar.hs-augsburg.de/w/index.php?title=Geordnetes_Paar:_Definition_von_Frege&oldid=52229“