Axis Aligned Bounding Box

Dieser Artikel erfüllt die GlossarWiki-Qualitätsanforderungen nur teilweise:

Korrektheit: 4 (großteils überprüft)

Umfang: 3 (einige wichtige Fakten fehlen)

Quellenangaben: 1 (fehlen großteils)

Quellenarten: 5 (ausgezeichnet)

Konformität: 5 (ausgezeichnet)

Definition (von Kowarschick)

zweidimensionale Bounding Box

Es sei $ o $ ein kompaktes (d. h. ein abgeschlossenes und beschränktes) geometrisches 2D- bzw. 3D-Objekt. Eine Axis Aligned Bounding Box (AABB) oder kurz Bounding Box ist ein spezieller Hüllkörper für das Objekt $ o $ in Form eines achsenparallelen Rechtecks (2D) bzw. Quaders (3D). Das Objekt $ o $ berührt alle 4 bzw. 6 Seiten der Bounding Box.

Eigenschaften

• Es gibt für jedes kompakte Objekt jeweils genau eine AABB. Dieses ist das kleinstmögliche achsenparallele Rechteck bzw. der kleinstmögliche achsenparallele Quader das bzw. der $ o $ einschließt. Es wird sogar die konvexe Hülle von $ o $ eingeschlossen.

• Die Bounding Box kann bei polygonalen Objekten sehr einfach über eine Minimums- und Maximumssuche über die Koordinaten aller Eckpunkte des Objektes ermittelt werden. Aber auch für andere geometrische Objekte, wie Kreise oder achsenparallele Ellipsen, ist die Ermittlung der AABB sehr einfach.

Integritätsbedingungen einer zwei-dimensionalen Bounding Box

Attribute einer zweidimensionalen Bounding Box

Es sei eine Bounding Box mit folgenden Attributen gegeben:

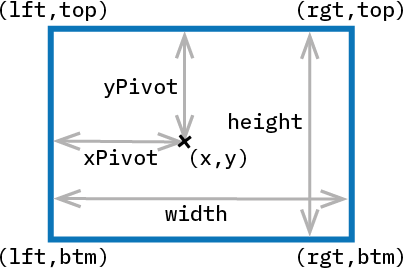
• lft: $ x $-Koordinate der beiden linken Ecken
• rgt: $ y $-Koordinate der beiden rechten Ecken
• top: $ x $-Koordinate der beiden oberen Ecken
• btm: $ y $-Koordinate der beiden unteren Ecken
• width: Breite der Bounding Box
• height: Höhe der Bounding Box
• x: $ x $-Koordinate des Ankerpunkts
• y: $ y $-Koordinate der Ankerpunkts
• xAnchor: Relativer Abstand der $ x $-Koordinate des Ankerpunkts vom linken Rand
• yAnchor: Relativer Abstand der $ y $-Koordinate des Ankerpunkts vom oberen Rand
• xPivot: Absoluter Abstand der $ x $-Koordinate des Ankerpunkts vom linken Rand (engl.: pivot = Drehpunkt)
• yPivot: Absoluter Abstand der $ y $-Koordinate des Ankerpunkts vom oberen Rand

Beachten Sie bitte, dass eine Bounding Box gemäß Definition nicht gedreht werden kann. (Wenn die Bounding Box einen Kreis umschließt und dieser gedreht wird, ändert sich Box nicht. Für andere Objekte gilt dies allerdings nicht. Jedesmal wenn beispielsweise ein Rechteck um ihren Ankerpunkt gedreht wird, müssen die Maße der zugehörigen Bounding Box angepasst werden.)

Eigentlich ist der Begriff pivot/Drehpunkt im Zusammenhang mit Bounding Boxes falsch. Allerdings wird die Position des Ankerpunkt eines geometrischen Objektes in vielen Werkzeugen (wie z. B. bei der Arbeitsfläche in Photoshop) und Grafikbibliotheken (wie z. B. pixi.js) mittels relativer Abstände hinsichtlich Breite und Höhe der Box von der linken oberen Ecke der Box aus gesehen angegeben. Wenn man den Abstand absolut (in Pixeln oder einer anderen Grafikeinheit) angeben will, muss man also einen alternativen Namen verwenden. Hier wird die pixi.js-Konvention beibehalten, den Begriff Pivot dafür zu verwenden, schon allein aus dem Grund, dass der Drehpunkt der eingeschlossenen Objektes mit den Ankerpunkt der Bounding Box zusammenfallen sollte.

Für eine Bounding Box gelten folgende Integritätsbedingungen (wenn man ein in der Computergrafik übliches Koordinatensystem zugrundelegt, bei dem sich der Null punkt in der linken oberen Ecke der Bühne befindet und die $ y $-Werte in Richtung unterem Bühnenrand größer werden):

• rgt >= lft
• btm >= top (Koordinatensystem!)
• width === rgt-lft >= 0
• height === btm-top >= 0 (Koordinatensystem!)
• lft === x-xPivot
• rgt === x-xPivot+width === lft+width
• top === y-yPivot
• btm === y-yPivot+height === top+height (Koordinatensystem!)
• xAnchor === xPivot/width
• yAnchor === yPivot/height

Kollisionserkennung

Zwei kollidierende Bounding Boxes

Zwei nicht kollidierende Bounding Boxes

Die Kollisionserkennung ist für Bounding Boxes relativ einfach. Daher geht man in der Computergrafik oft zweistufig vor. Im ersten Schritt überprüft man, ob sich zwei Bounding Boxes berühren oder überlappen. Falls dies nicht der Fall ist, berühren oder überlappen sich die zugehörigen Objekte ebenfalls nicht. Das heißt, in diesem Fall liegt mit Sicherheit keine Kollision vor. Dieser Fall tritt sehr häufig ein, wenn sich viele relativ kleine Objekte auf der Bühne befinden. Falls die Bounding Boxes kollidieren, ist damit allerdings noch nicht gesagt, das auch die darin enthaltenen Objekte kollidieren. Das heißt, in diesem Fall müssen i. Allg. weitere mathematische Tests unternommen, um festzustellen, ob die beiden in den Boxen eingeschlossenen Objekte kollidieren. Falls dies der Fall ist, schließt sich daran üblicherweise die Kollisionsbehandlung an.

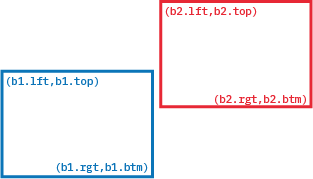
Um eine Formel für die Kollisionserkennung zweier Bounding Boxes b1 und b2 herzuleiten, ist es von Vorteil sich zunächst den gegenteiligen Fall anzusehen: Die Boxes überlappen sich genau dann nicht, wenn der linke Rand einer Box größer ist als der rechte der anderen oder der obere Rand der einen größer ist als der untere der anderen. Damit hat man folgende Bedingung:

if (b1.left > b2.rgt || b2.lft > b1.rgt || b1.top > b2.btm || b2.top > b1.btm)
{ <b1 und b2 kollidieren nicht> }

Wenn man diese Aussage negiert, erhält man einen Kollisionstest (man beachte den Negationsoperator !):

if (!(b1.left > b2.rgt || b2.lft > b1.rgt || b1.top > b2.btm || b2.top > b1.btm))
{ <b1 und b2 kollidieren> }

Nach dem De-Morganschen-Gesetz !(a || b) === !a && !b kann man diesen Test folgendermaßen vereinfachen:

if (b1.left <= b2.rgt && b2.lft <= b1.rgt && b1.top <= b2.btm && b2.top <= b1.btm)
{ <b1 und b2 kollidieren> }

Modifikation des Pivotpunkts

Verschiebung des Pivotpunktes

Wenn man den Pivotpunkt der Bounding Box verschieben will, ohne die Box selbst zu verschieben, muss man eine Ausgleichrechnung durchführen.

Wie man dem nebenstehenden Bild entnehmen kann, verschiebt sich der Pivotpunkt x um den Betrag xPivot_neu-xPivot_alt. Wenn nun lft_neu === lft_alt (und damit auch rgt_neu === rgt_alt) gelten soll, kommt die Integritätsbedingung lft === x-xPivot zur Anwendung:

0 === lft_neu - lft_alt
  === (x_neu - xPivot_neu) - (x_alt - x_Pivot_alt) 
  === x_neu - x_alt - (xPivot_neu - xPivot_alt)

Also gilt die Beziehung

x_neu === x_alt + (xPivot_neu - xPivot_alt)

Eine analoge Rechnung ergibt sich für y_neu.

Wenn dagegen der Ankerpunkt absolut gesehen an derselben Stelle der Bühne verbleiben soll, wenn also x_neu === x_alt und y_neu === y_alt gelten soll, muss man die Ränder der Bounding Box verschieben. Es kommt wieder die Integritätsbedingung lft === x-xPivot, d. h. x === lft+xPivot zur Anwendung:

0 === x_neu - x_alt
  === (lft_neu + xPivot_neu) - (lft_alt + x_Pivot_alt) 
  === lft_neu - lft_alt + (xPivot_neu - xPivot_alt)

Also gilt hier die Beziehung

lft_neu === lft_alt - (xPivot_neu - xPivot_alt)

Wie man an diesen Beispielen sehr schön sieht, kann man aus den zuvor angegebenen Integritätsbedingungen sehr einfach Formeln ableiten, wie man in bestimmten Situationen bei der Änderung eines Wertes andere Werte automatisch anpassen kann. Welche der Formeln zum Einsatz kommt, hängt vom jeweiligen Einsatzzweck ab.

Siehe auch

• Einhüllende Kurve
• Hüllkörper