Binokulares Sehen
Dieser Artikel erfüllt die GlossarWiki-Qualitätsanforderungen nicht:
| Korrektheit: 0 (nicht überprüft) |
Umfang: 1 (zu gering) |
Quellenangaben: 0 (fehlen vollkommen) |
Quellenarten: 0 (ungenügend) |
Konformität: 0 (ungenügend) |
Dieser Eintrag soll kurz erklären, wie das binokulare Tiefensehen beim Menschen funktioniert.
Das Auge eines Wirbeltieres bzw. eines Menschen projeziert den Sichtbereich auf die kugelförmige Innenseite des Augapfels, die Retina (siehe Abbildung 1). Diese ist vollständig mit Sinneszellen, sogenannten Rezeptoren bedeckt, welche unterteilt werden in Zellen zur Farbwahrnehmung, den Zäpfchen und Zellen zur Helligkeitswahrnehmung, den Stäbchen.
[Abbildung 1: netzhautgrupe.jpg | Beschriftung: Querschnitt des Auges]
Zwar ist die komplette Netzhaut mit Rezeptoren bedeckt, jedoch ist die Verteilung dieser nicht homogen, sondern ortsabhängig. Die Zapfen stehen in der zentralsten Stelle der Retina, der Netzhautgrube (Siehe Abbildung 1, Kürzel NG), in großer Dichte beieinander. Die Netzhautgrube hat einen Radius von ein bis zwei Millimeter und enthällt etwa 130000 Zäpfchen und annähernd keine Stäbchen. Bei genügend Lichteinfall, wenn man also mit den Zäpfchen sehen kann, konzentriert sich das Sehen also auf die Netzhautgrube, die etwa 0,02\% der Netzhautfläche ausmacht. Das entspricht etwa zwei Grad unseres rund 200 Grad umfassenden horizontalen Blickfeldes. Wir sehen also eigentlich nur den Ausschnitt scharf, den unsere beiden Augen mit ihren Sehachsen fixieren.
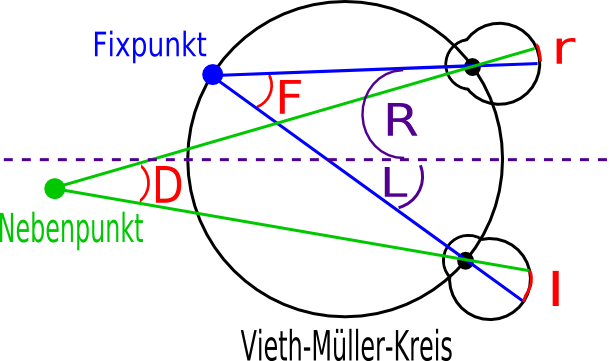
Abbildung 2 zeigt einen vereinfachten zweidiminsionalen Fall eines Blickes. Die beiden Augen fixieren einen Punkt, den Fixpunkt. Das heißt, dass das Bild des Fixpunktes mittig in der Netzhautgrube liegt.
Der Nebenpunkt, ein Punkt, der sich in der Nähe des Fixpunktes befindet, wird in die Nähe des Bildpunktes vom Fixpunkt projeziert. Die Disparität d, in der Optik auch Querdisparation genannt, ist definiert als d=r-l, wobei r der Winkel ist, der durch die Projektionsstrahlen von Fixpunkt und Nebenpunkt im rechten Auge entsteht und l der entsprechende Winkel im linken Auge ist.
Alle Nebenpunkte, die sich auf dem Kreis befinden der durch den Fixpunkt und die beiden Augenlinsen festgelegt ist, dem sogenannten Vieth-Müller-Kreis, besitzen somit die Disparität 0. Für alle Punkte innehalb dieses Kreises ist die Disparität positiv und für die Punkte auserhalb ist sie negativ.
Wie man aus Abbildung 3 erkennen kann, erzeugen alle Punkte, die auf dem Vieth-Müller- Kreis liegen die gleichen Bilder in beiden Augen. Von diesem Kreis abweichende Punkte erzeugen unterscheidliche Bilder und können sogar in einer verschiedenen Reihenfolge auf die Netzhäute projeziert werden.
Im Dreidimensionalen ist dieser Sachverhalt komplizierter aber vom Prinzip gleich. Die Menge aller Punkte der Disparität 0 formt jetzt keinen Kreis, sondern eine Fläche, den sogenannten Horopter, oder auch Sehbegrenzung genannt. Alle Nebenpunkte, die auf diesem Horopter liegen, erzeugen den gleichen visuellen Eindruck, das heißt die gleichen Bilder in beiden Augen.
Benutzt man als Koordinatensystem für die Bildpunkte ein Koordinatennetz, dessen Achsenkreuz durch das Zentrum der Netzhautgrube verläuft, so haben die Bildpunkte von Objektpunkten, die auf dem Horopter liegen, die gleichen Koordinaten in beiden Augen. Solche Punkte werden Deckpunkte genannt und vom Gehirn zu einem Punkt verschmolzen. Dieser Prozess wird Fusion genannt. Vorraussetzung dafür ist, dass sich die Sehachsen beider Augen exakt im fixierten Punkt kreuzen. Dies geschieht durch den sogenannten Fusionszwang, ein Reflex, der dafür sorgt, dass beide Augen ständig gleiche Punkte fixieren.
Alle Nebenpunkte, die eine Disparität ungleich 0 besitzen, also unterschiedliche Koordinaten haben, werden nicht zu einem Bildpunkt verschmolzen und erzeugen somit ein Doppelbild. Nun müßte man denken, dass es eine wahre Flut an Doppelbildern geben müßte, da sich nur sehr wenige Punkte einer Szene exakt auf dem Horopter befinden.
In der Physiologie des Sehens weiß man, dass zur Fusion zweier Bildpunkte diese nicht unbedingt auf korrespondierenden Netzhautstellen mit gleichen Koordinaten liegen müßen. Es genügt, dass sie in einem vom Netzhautort abhängigen Bereich um die korrespondierenden Stellen herum, dem Panum-Bereich liegen. Der Panumbereich ist in der Netzhautgrube kleiner als auf dem Rest der Netzhaut und hat immer die Form einer Ellipse, deren horizontale Achse größer ist als die vertikale. Gegenstände, die sich ein wenig vor oder hinter dem fixierten Objekt befinden, werden Dank des Panum-Bereichs also trotzdem noch beidäugig einfach gesehen, ohne ein Doppelbild zu erzeugen.
Aus der Existenz der Panum-Bereiche folgt, dass der Horopter keine scharfe Begränzung darstellt, sondern eine Breite hat. Alle Nebenpunkte die innerhalb des Horopters liegen können fusioniert werden. Will man das menschliche Sehen maschinell nachbilden, kann man, aus der Form des Horopters unmittelbar Einschränkungen für die Suche nach korrespondierenden Bildpunkten treffen.
Erst die räumliche Ausdehnung des Horopters macht einen Tiefeneindruck möglich. Die Fusion von Nebenpunkten, die keine Deckungspunkte sind, haben eine Disparität ungleich Null und damit eine wahrgebommene Tiefe in Bezug auf den Fixpunkt. Zwei leicht unterschiedliche Einzelbilder auf den Netzhäuten werden schließlich zu einem räumlichen Gesamtbild fusioniert.
Objektpunkte, die sich außerhalb des Horopters befinden, ergeben zwar Doppelbilder, doch werden diese kaum wahrgenommen. Das liegt daran, dass sich deren Bildpunkte meistens außerhalb der Netzhautgrube befinden und daher einerseits wegen der sehr geringen Zäpfchenauflösung nur unscharf wahrgenommen werden und andererseits die ihnen zugewandte Aufmerksamkeit gering ist.
Die kleinste wahrnehmbare Disparität entspricht beim Menschen etwa fünf bis zehn Winkelsekunden. Dieser Wert grenzt an der maximalen Auflösung der Augen. Ein Mensch kann also Tiefenwerte fusionierter Nebenpunkte in Bezug auf den Fixpunkt sehr genau wahrnehmen. Um allerdings die absoluten Tiefenwerte, also die Distanz eines Fixpunktes zu den Augen zu schätzen, muß die Augenstellung, also die Winkel R und L aus Abbildung 2 bekannt sein. Wundt und Helmholtz zeigten vor fast 100 Jahren, dass diese Winkel vom Nervensystem des Menschen nicht sehr genau bestimmt werden können. Ein Mensch kann also absolute Tiefenwerte nur schlecht abschätzen.
In diesem Kapitel wurde erklärt, dass man nur etwa in einem Winkel von 2° scharf sehen kann und außerdem nur alle Punkte des Horopters einen räumlichen Eindruck erzeugen. Somit könnte ein Mensch immer nur Ausschnitte eines Objektes sehen, nie aber ein Gesamtbild erhalten. Die Augen rücken uns daher im zeitlichen Abstand von 0,2 Sekunden bis 0,6 Sekunden, meist unbewußt, nacheinander verschiedene Ausschnitte eines Gegenstandes vor die Netzhautgrube, um dem betrachter letztendlich ein scharfes räumliches Gesamtbild zu geben.
links
http://en.wikipedia.org/wiki/Stereoscopic
http://de.wikipedia.org/wiki/Stereoskopisches_Sehen
http://en.wikipedia.org/wiki/Binocular_vision
Anmerkung
Dieser Artikel wurde von FHAWiki:Binokulares Sehen hierher verschoben.