Kritischer Pfad und Kritische Kette (Vergleich): Unterschied zwischen den Versionen
Kowa (Diskussion | Beiträge) |
Kowa (Diskussion | Beiträge) |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
| style="vertical-align:top;" | | | style="vertical-align:top;" | | ||
<big>''' | <big>'''Vorgangspuffer (im Netzplan implizit enthalten)'''</big> | ||
Statistische Fluktuationen werden im Allgemeinen nur im Form von Pufferzeiten | Statistische Fluktuationen werden im Allgemeinen nur im Form von Pufferzeiten | ||
| Zeile 27: | Zeile 27: | ||
| style="vertical-align:top;" | | | style="vertical-align:top;" | | ||
<big>''' | <big>'''Projektpuffer (explizit berechnet für Vorgangsfolgen)'''</big> | ||
Statistische Fluktuationen werden als unabänderlich angesehen und daher | Statistische Fluktuationen werden als unabänderlich angesehen und daher | ||
| Zeile 41: | Zeile 41: | ||
⇒ Paradigmenwechsel; die explizite Verwaltung von Puffer für kritische Vorgänge hat deutliche | ⇒ Paradigmenwechsel; die explizite Verwaltung von Puffer für kritische Vorgänge hat deutliche | ||
Auswirkungen auf die Tätigkeiten des Projektleiters. | Auswirkungen auf die Tätigkeiten des Projektleiters. | ||
|- | |||
| style="vertical-align:top;" | | |||
<big>'''Schätzungen erfolgen tages- oder stundengenau'''</big> | |||
Projektmanager sind häufig der Meinung, dass eine stundengenaue Schätzung präzisere Ergebnisse liefert als eine tagesgenaue. | |||
| style="vertical-align:top;" | | |||
<big>'''Schätzungen erfolgen stets tagesgenau'''</big> | |||
Dies ist allerdings ein Irrtum. Funktionspunkte unterschiedlicher Projekte streuen mehr, wenn man sie stundengenau und nicht tagesgenau ermittelt. Eine Person leistet in 10 Stunden {{iAllg}} nicht mehr als in 8, da sie gegen Ende eines Arbeitstages durch Konzentrationsprobleme mehr Fehler macht, die mit zusätzlichem Zeitaufwand wieder ausgebügelt werden müssen. Daher lautet auch ein Prinzip von [[Extrem Programming]]: „keine Überstunden“. Durch Überstunden sinkt die Produktivität. | |||
|- | |- | ||
| Zeile 60: | Zeile 72: | ||
Die [[Puffer|Einzelpuffer]] werden bei kritischen Vorgängen als [[Gesamtpuffer]] an das Projektende angefügt. | Die [[Puffer|Einzelpuffer]] werden bei kritischen Vorgängen als [[Gesamtpuffer]] an das Projektende angefügt. | ||
Für nicht-kritische Vorgänge werden die | Für nicht-kritische Vorgänge werden die Einzelpuffer ebenfalls zu einem Puffer zusammengefasst | ||
und direkt vor einem kritischen Vorgang als so genannte [[Zubringerpuffer]] eingefügt. | und direkt vor einem kritischen Vorgang als so genannte [[Zubringerpuffer]] eingefügt. | ||
| Zeile 220: | Zeile 232: | ||
| align="right" | 11 || Projektende || 10 || || || || || || || || || | | align="right" | 11 || Projektende || 10 || || || || || || || || || | ||
|} | |} | ||
'''Achtung''': Die Werte μ und σ wurden mittels Mathcad mit Hilfe der [[Beta-Verteilung]] ermittelt. Es wurde weder die Dreiecks- noch die PERT-Verteilung benutzt. Die Beta-Verteilung ist für die Schätzung besser geeignet als Dreieck- und Pert-Verteilung. | |||
Um zu dieser Tabelle zu gelangen wurden folgende Schritte durchgeführt: | Um zu dieser Tabelle zu gelangen wurden folgende Schritte durchgeführt: | ||
| Zeile 227: | Zeile 241: | ||
<li>[[Netzwerk (Projektmanagement)|Netzwerkplanung]]: Festlegung von [[Ende-Anfang-Beziehung]]en zwischen den Vorgängen (Spalte „Vorgänger“)</li> | <li>[[Netzwerk (Projektmanagement)|Netzwerkplanung]]: Festlegung von [[Ende-Anfang-Beziehung]]en zwischen den Vorgängen (Spalte „Vorgänger“)</li> | ||
<li>[[Ressourcenplanung]]: Festlegung des benötigten Mitarbeiter (Spalte „Ressourcen“)</li> | <li>[[Ressourcenplanung]]: Festlegung des benötigten Mitarbeiter (Spalte „Ressourcen“)</li> | ||
<li>[[Schätzung|Dreipunkt-Schätzung]]: Schätzung der Dauer der einzelnen Vorgänge (restliche Spalten)</li> | <li>[[Schätzung|Dreipunkt-Schätzung]]: Schätzung der Dauer der einzelnen Vorgänge (restliche Spalten) unter der Annahme, dass ''alle eingeplanten Mitarbeiter jeweils '''gemeinsam''' am entsprechenden Vorgang arbeiten''</li> | ||
</ol> | </ol> | ||
| Zeile 246: | Zeile 260: | ||
Wahrscheinlichkeit, dass ein Vorgang, fristgerecht fertig gestellt wird. Im klassischen Projektplan wird dagegen eine längere Dauer eingetragen. Daher besteht hier (in diesem fiktiven Beispiel) eine ca. 98-prozentige Wahrscheinlichkeit, dass ein Vorgang fristgerecht abgeschlossen wird. In der letzten Spalte der Tabelle ist jeweils die Differenz zwischen der konservativen und CCPM-Schätzung aufgeführt. Man sieht, dass die diese Differenz zwischen einem und vier Tagen beträgt. | Wahrscheinlichkeit, dass ein Vorgang, fristgerecht fertig gestellt wird. Im klassischen Projektplan wird dagegen eine längere Dauer eingetragen. Daher besteht hier (in diesem fiktiven Beispiel) eine ca. 98-prozentige Wahrscheinlichkeit, dass ein Vorgang fristgerecht abgeschlossen wird. In der letzten Spalte der Tabelle ist jeweils die Differenz zwischen der konservativen und CCPM-Schätzung aufgeführt. Man sieht, dass die diese Differenz zwischen einem und vier Tagen beträgt. | ||
Die größere Unsicherheit bezüglich der fristgerechten Beendigung eines jeden Vorgangs wird in CCPM durch zusätzliche Angabe eines expliziten Puffers – des so genannten Projektgesamtpuffers – am Ende des | Die größere Unsicherheit bezüglich der fristgerechten Beendigung eines jeden Vorgangs wird in CCPM durch zusätzliche Angabe eines expliziten Puffers – des so genannten Projektgesamtpuffers – am Ende des Projekts kompensiert. | ||
===Klassisches Projektmanagement (mit möglicher Ressourcenüberlastung)=== | ===Klassisches Projektmanagement (mit möglicher Ressourcenüberlastung)=== | ||
| Zeile 292: | Zeile 306: | ||
Die zweifache Summe der zugehörigen Streuungen entspricht in etwa der Summe der Differenzen zwischen den konservativen Schätzungen und den Fifty-fifty-Schätzungen. (Die Abweichung kommt daher, das im Beispiel die konservativen Schätzwerte auf ganze Tage gerundet wurden.) | Die zweifache Summe der zugehörigen Streuungen entspricht in etwa der Summe der Differenzen zwischen den konservativen Schätzungen und den Fifty-fifty-Schätzungen. (Die Abweichung kommt daher, das im Beispiel die konservativen Schätzwerte auf ganze Tage gerundet wurden.) | ||
Die Differenz zwischen den beiden Schätzungen kann man als Projektpuffer ans Projektende einfügen (siehe lila Markierung – kurzer Strich). Damit ändert sich nicht die Gesamtlaufzeit des | Die Differenz zwischen den beiden Schätzungen kann man als Projektpuffer ans Projektende einfügen (siehe lila Markierung – kurzer Strich). Damit ändert sich nicht die Gesamtlaufzeit des Projekts, aber dennoch hat man schon etwas gewonnen: | ||
* Das [[Studentensyndrom]] und das [[Parkinsonsche Gesetz]] („Arbeit dehnt sich in genau dem Maß aus, wie Zeit für ihre Erledigung zur Verfügung steht“) kommen weniger zum Tragen. | * Das [[Studentensyndrom]] und das [[Parkinsonsche Gesetz]] („Arbeit dehnt sich in genau dem Maß aus, wie Zeit für ihre Erledigung zur Verfügung steht“) kommen weniger zum Tragen. | ||
* Es wird zwischen einem internen und einem externen Projektende unterschieden (siehe lila Markierungen – Kringel). Der dazwischenliegende Zweitraum dient als Puffer gegen unvorhergesehene Ereignisse. | * Es wird zwischen einem internen und einem externen Projektende unterschieden (siehe lila Markierungen – Kringel). Der dazwischenliegende Zweitraum dient als Puffer gegen unvorhergesehene Ereignisse. | ||
| Zeile 327: | Zeile 341: | ||
|- | |- | ||
! style="vertical-align:top"| Projektgesamtpuffer<br/>gemäß Zentralem Grenzwertsatz | ! style="vertical-align:top"| Projektgesamtpuffer<br/>gemäß Zentralem Grenzwertsatz | ||
| $2\sqrt{σ_2^2+σ_3^2+σ_4^2+σ_6^2+σ_7^2+σ_{10}^2} = $<br/>$2\sqrt{0,4^2+1,9^2+0,4^2+1,4^2+0,4^2+0,3^2}$ || $\approx 4,96$ || $\approx 5$ | | $2\times\sqrt{σ_2^2+σ_3^2+σ_4^2+σ_6^2+σ_7^2+σ_{10}^2} = $<br/>$2\times\sqrt{0,4^2+1,9^2+0,4^2+1,4^2+0,4^2+0,3^2}$ || $\approx 4,96$ || $\approx 5$ | ||
|- | |- | ||
! style="vertical-align:top"| Zubringerpuffer 1<br/>gemäß Zentralem Grenzwertsatz | ! style="vertical-align:top"| Zubringerpuffer 1<br/>gemäß Zentralem Grenzwertsatz | ||
| $3\sqrt{σ_5^2} = 3\sqrt{1,1^2}$ || $=3,3$ || $\approx 3$ | | $3\times\sqrt{σ_5^2} = 3\times\sqrt{1,1^2}$ || $=3,3$ || $\approx 3$ | ||
|- | |- | ||
! style="vertical-align:top"| Zubringerpuffer 2<br/>gemäß Zentralem Grenzwertsatz | ! style="vertical-align:top"| Zubringerpuffer 2<br/>gemäß Zentralem Grenzwertsatz | ||
| $3\sqrt{σ_8^2+σ_9^2} = 3\sqrt{0,4^2+0,4^2}$ || $\approx 1,70$ || $\approx 2$ | | $3\times\sqrt{σ_8^2+σ_9^2} = 3\times\sqrt{0,4^2+0,4^2}$ || $\approx 1,70$ || $\approx 2$ | ||
|} | |} | ||
Aktuelle Version vom 26. Juni 2024, 16:01 Uhr
Dieser Artikel erfüllt die GlossarWiki-Qualitätsanforderungen nur teilweise:
| Korrektheit: 4 (großteils überprüft) |
Umfang: 4 (unwichtige Fakten fehlen) |
Quellenangaben: 4 (fast vollständig vorhanden) |
Quellenarten: 3 (gut) |
Konformität: 3 (gut) |
Vergleich
| Methode des kritischen Pfades (Critical Path Method, CPM; Metra Potential Method, MPM) | Methode der kritischen Kette (Critical Chain Project Management, CCPM) |
|---|---|
|
Vorgangspuffer (im Netzplan implizit enthalten) Statistische Fluktuationen werden im Allgemeinen nur im Form von Pufferzeiten in den einzelnen Vorgängen beachtet. Man unterschiedet zwischen:
|
Projektpuffer (explizit berechnet für Vorgangsfolgen) Statistische Fluktuationen werden als unabänderlich angesehen und daher bei der Planung und Projektverlauf von Anfang an berücksichtigt. Der Puffer wird dabei nicht einzelnen Vorgängen zugeordnet, sondern einer Kette von aufeinander folgenden Vorgängen. Man unterschiedet zwischen:
⇒ Paradigmenwechsel; die explizite Verwaltung von Puffer für kritische Vorgänge hat deutliche Auswirkungen auf die Tätigkeiten des Projektleiters. |
|
Schätzungen erfolgen tages- oder stundengenau Projektmanager sind häufig der Meinung, dass eine stundengenaue Schätzung präzisere Ergebnisse liefert als eine tagesgenaue. |
Schätzungen erfolgen stets tagesgenau Dies ist allerdings ein Irrtum. Funktionspunkte unterschiedlicher Projekte streuen mehr, wenn man sie stundengenau und nicht tagesgenau ermittelt. Eine Person leistet in 10 Stunden i. Allg. nicht mehr als in 8, da sie gegen Ende eines Arbeitstages durch Konzentrationsprobleme mehr Fehler macht, die mit zusätzlichem Zeitaufwand wieder ausgebügelt werden müssen. Daher lautet auch ein Prinzip von Extrem Programming: „keine Überstunden“. Durch Überstunden sinkt die Produktivität. |
|
Geschätzte Vorgangsdauer enthält i. Allg. Puffer Die Dauer eines Vorgangs wird so geschätzt, dass der Vorgang innerhalb der geschätzten Zeit mit großer Wahrscheinlichkeit beendet wird (mindestens 80%, meist jedoch deutlich mehr: 90%, 95%, 99%). Das heißt, alle Einzelschätzungen enthalten implizit einen eigenen Puffer, um statistische Fluktuationen abzufangen. |
Geschätzte Vorgangsdauer enthält keinen Puffer Die Dauer eines Vorgangs wird so geschätzt, dass dieser Vorgang innerhalb der geschätzten Zeit lediglich mit ca. 50%-iger Wahrscheinlichkeit beendet wird (Erwartungswert ≈ Median). Die Einzelpuffer werden bei kritischen Vorgängen als Gesamtpuffer an das Projektende angefügt. Für nicht-kritische Vorgänge werden die Einzelpuffer ebenfalls zu einem Puffer zusammengefasst und direkt vor einem kritischen Vorgang als so genannte Zubringerpuffer eingefügt. Aufgrund statistischer Gesetze (Zentraler Grenzwertsatz der Statistik) können der Gesamtpuffer und die Zubringerpuffer i. Allg. deutlich kürzer gewählt werden, als die Summe der jeweils zugehörigen impliziten Einzelpuffer. ⇒ Zeitgewinn Bis heute ist es allerdings nicht gelungen, ein Verfahren zu entwickeln, mit dem sich ein in statistischer Hinsicht „optimaler“ Zeitplan erstellen lässt. Daher gibt sich CCPM damit zufrieden, einen möglichst guten Zeitplan zu erstellen, da auch dies einen Zeitgewinn zur Folge hat. |
|
Früher Beginn von nicht-kritischen Vorgängen Nicht-kritische Vorgänge werden häufig so früh wie möglich begonnen. Das heißt, die Vorgangspuffer-Zeiten, (Freier Puffer und Vorgangsgesamtpuffer), die sich durch die Rückwärtsrechnung ergeben, werden auch ausgenutzt. |
Später Beginn von nicht-kritischen Vorgängen Nicht-kritische Vorgänge sollen möglichst immer so spät wie möglich begonnen werden. Der Starttermin wird i. Allg. nach hinten verschoben. Dabei wird allerdings genügend Puffer (z. B. mit Hilfe des zentralen Grenzwertsatzes) am Ende einer Kette von nicht-kritischen Vorgängen eingeplant (Zubringerpuffer), damit der (evtl. kritische) Vorgang, der die Ergebnisse dieser sogenannten Zubringerkette benötigt, nach Möglichkeit nicht verzögert wird. Vorteile der Verschiebung des Starttermins:
|
|
Vorgänge werden termingerecht beendet oder später Vorgänge werden termingerecht beendet oder – bei unerwarteten Problemen – später. Trotz der großen Einzelpuffer werden Vorgänge i. Allg. nicht früher beendet. Gründe:
|
Vorgänge werden häufig auch vorzeitig beendet Vorgänge werden vor, zum oder nach dem gesetzten Termin beendet. Für die Mitarbeiter gibt es keine festen Terminvorgaben, sondern nur die Vorgabe, einen Vorgang so schnell wie möglich zu beenden, ohne Abstriche an Funktionalität oder Qualität zu machen. Mitarbeiter dürfen dabei nicht unter Druck gesetzt werden, insbesondere Überstunden sind nur in Ausnahmefällen zulässig. ⇒ Zeitgewinn bei früher, termingerecht oder nur leicht verspätet beendeten Vorgängen (da die Vorgangsdauer kürzer als bei CPM geschätzt wird). |
|
Multitasking ist NICHT verpönt Es wird häufig Multitasking, d.h. der gleichzeitige Einsatz von Mitarbeitern (oder anderen Ressourcen) in mehreren Vorgängen oder Projekten, betrieben. Dies geschieht vor allem, um jede Ressource so gut wie möglich auszulasten. Insbesondere kommt es oft zu Planungen, bei denen eine Ressource in mehreren parallel laufenden Vorgängen jeweils zu 100% verplant ist (fehlendes Resource Leveling). Derartige Vorgänge werden normalerweise nicht termingerecht beendet. |
Multitasking ist verpönt Multitasking wird grundsätzlich vermieden, d.h., Resource Leveling ist Pflicht. ⇒ Zeitgewinn, da Multitasking jeden Einzelvorgang bis auf den letzten verzögert. ⇒ nochmals Zeitgewinn, da der Overhead, der durch Aufgabenwechsel entstehen würde, entfällt. |
|
KEINE Entlastung bei Arbeit an kritischen Vorgängen Mitarbeiter, die an kritischen Vorgängen arbeiten, werden nicht vom Tagesgeschäft entlastet. |
Entlastung bei Arbeit an kritischen Vorgängen Mitarbeiter, die an kritischen Vorgängen arbeiten, werden vom Tagesgeschäft entlastet (wenig Telefon, kaum E-Mails, keine anderen Aufgaben etc.). ⇒ Zeitgewinn |
|
Einpunkt-Schätzmethode Für jeden Vorgang wird die Dauer als fester Wert geschätzt und festgelegt. |
Dreipunkt-Schätzmethode Für die Schätzung der Dauer von Einzelvorgängen wird die Dreipunkt-Schätzmethode (kürzeste Dauer, wahrscheinliche Dauer, längste Dauer) eingesetzt, um für jeden Vorgang sowohl einen guten Schätzwert für die eigentliche Dauer (Erwartungswert), als auch für einen notwendigen Puffer (n mal Standardabweichung) zu ermitteln. (Diese Methode wurde ursprünglich auch in PERT eingesetzt.) |
|
Parallele kritische Vorgänge sind erlaubt Der kritische Pfad ist nicht notwendig immer ein Pfad. In Ausnahmefällen kann es auch kritische Vorgänge geben, die parallel laufen. |
Parallele kritische Vorgänge sind NICHT erlaubt Um den zentralen Grenzwertsatz der Statistik anwenden zu können, wird formal verlangt, dass es keine parallelen kritischen Vorgänge gibt. Sollte es parallele Zweige von kritischen Vorgängen geben, wird ein Zweig als kritisch definiert und die anderen als nicht-kritisch. Die neuen nicht-kritischen Pfade gelten fortan als Zubringerpfade. Da für den zugehörigen Zubringerpuffer kein Platz im Pfad vorhanden ist, muss der Puffer bei der Berechnung des Nachfolger-Pfades berücksichtigt werden (allerdings gibt es dafür bislang keine Methode, die mathematisch fundiert wäre – hier muss der Projektleiter selbst plausible Werte für die Puffervergrößerung festlegen). ⇒ Diese künstliche Unterscheidung von kritischen und als nicht-kritisch festgelegte kritischen Vorgängen ist rein technischer Natur und bringt sonst keinerlei Vorteile. Dieser Spezialfall tritt außerdem nur selten ein. |
Beispiel
Gegeben sei folgendes fiktive Projekt zur Erstellung eines Web-Auftritts der „Metzgerei Meier“:
| Nr. | Vorgang | Vorgänger | Ressourcen | min. | real. | max. | $μ$ | $σ$ | $μ +2σ$ | kons. | kons. $-$ $μ$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Projektstart | ||||||||||
| 2 | Konzeption | 1 | Designer, Informatiker | 2 | 3 | 6 | 3 | 0,4 | 3,8 | 4 | 1 |
| 3 | Gestaltung Wireframes | 2 | Designer | 4 | 5 | 20 | 7 | 1,9 | 10,8 | 11 | 4 |
| 4 | Gestaltung Style | 3 | Designer; Informatiker | 2 | 4 | 6 | 4 | 0,4 | 4,8 | 5 | 1 |
| 5 | Implementierung Backend | 2 | Informatiker | 2 | 3 | 12 | 4 | 1,1 | 6,2 | 6 | 2 |
| 6 | Implementierung Frontend | 3, 5 | Informatiker | 3 | 4 | 15 | 5 | 1,4 | 7,8 | 8 | 3 |
| 7 | Implementierung Style | 4, 6 | Designer; Informatiker | 1 | 2 | 5 | 2 | 0,4 | 2,8 | 3 | 1 |
| 8 | Contenterstellung: Text | 1 | Redakteur | 2 | 3 | 5 | 3 | 0,4 | 3,8 | 4 | 1 |
| 9 | Contenterstellung: Bild | 8 | Redakteur | 1 | 2 | 3 | 2 | 0,4 | 2,8 | 3 | 1 |
| 10 | Integration | 4, 7, 9 | Designer, Informatiker, Redakteur | 2 | 2 | 3 | 2 | 2,6 | 0,3 | 3 | 1 |
| 11 | Projektende | 10 |
Achtung: Die Werte μ und σ wurden mittels Mathcad mit Hilfe der Beta-Verteilung ermittelt. Es wurde weder die Dreiecks- noch die PERT-Verteilung benutzt. Die Beta-Verteilung ist für die Schätzung besser geeignet als Dreieck- und Pert-Verteilung.
Um zu dieser Tabelle zu gelangen wurden folgende Schritte durchgeführt:
- Aktivitätstrukturplanung: Festlegung der einzelnen Vorgänge (Spalte „Vorgang“)
- Netzwerkplanung: Festlegung von Ende-Anfang-Beziehungen zwischen den Vorgängen (Spalte „Vorgänger“)
- Ressourcenplanung: Festlegung des benötigten Mitarbeiter (Spalte „Ressourcen“)
- Dreipunkt-Schätzung: Schätzung der Dauer der einzelnen Vorgänge (restliche Spalten) unter der Annahme, dass alle eingeplanten Mitarbeiter jeweils gemeinsam am entsprechenden Vorgang arbeiten
Im klassischen Projektmanagement wird zur Ermittlung der Dauer eines Vorgangs üblicherweise eine Einpunkt-Schätzung durchgeführt. Eine Methode ist beispielsweise die Expertenschätzung (Delphi-Methode, Planning Poker). Hierbei versuchen sich Experten für jeden Vorgang auf einen Wert zu einigen.
In CCPM wird zur Schätzung der Dauer eines Vorgangs dagegen mit Dreipunkt-Schätzungen gearbeitet (ursprünglich wurde diese Vorgehensweise für PERT vorgeschlagen). Bei einer Dreipunkt-Schätzung müssen sich die Experten für jeden Vorgang auf drei Werte einigen: bester Fall (min.), wahrscheinlichster Fall (realistisch, real.), schlechtester Fall (max.). Daraus werden der Erwartungswert $μ$ und die Streuung $σ$ einer geeigneten Wahrscheinlichkeitsverteilung (wie beispielsweise der Dreiecksverteilung oder der Beta-Verteilung) ermittelt. Der Erwartungswert $μ$ gibt den Zeitpunkt an, zu dem der zugehörige Vorgang ca. mit 50 % Wahrscheinlichkeit abgeschlossen ist. Zu diesem Wert kann man das $n$-fach von $σ$ addieren, um die Wahrscheinlichkeit für eine rechtzeitige Beendigung eines Vorgangs zu erhöhen. In $μ + 1σ$ Tagen kann ein Vorgang beispielsweise mit einer Wahrscheinlichkeit von ca. 84 % beendet werden, in $μ + 2σ$ Tagen mit einer Wahrscheinlichkeit von ca. 98 %.
Im Beispiel wurden keine echten Expertenschätzungen durchgeführt, sondern einfach fiktive Werte für die Dreipunkt-Schätzungen eingetragen.
Im Critical-Path-Projektmanagement (CPM) wird als Dauer eines Vorgangs der Wert $μ$ angenommen (erste gelbe Spalte). Die konservativen Schätzwerte für die klassische Projektplanung wurden durch Runden von $μ + 2σ$ ermittelt (zweite gelbe Spalte). Das heißt, in CCPM besteht eine lediglich 50-prozentige Wahrscheinlichkeit, dass ein Vorgang, fristgerecht fertig gestellt wird. Im klassischen Projektplan wird dagegen eine längere Dauer eingetragen. Daher besteht hier (in diesem fiktiven Beispiel) eine ca. 98-prozentige Wahrscheinlichkeit, dass ein Vorgang fristgerecht abgeschlossen wird. In der letzten Spalte der Tabelle ist jeweils die Differenz zwischen der konservativen und CCPM-Schätzung aufgeführt. Man sieht, dass die diese Differenz zwischen einem und vier Tagen beträgt.
Die größere Unsicherheit bezüglich der fristgerechten Beendigung eines jeden Vorgangs wird in CCPM durch zusätzliche Angabe eines expliziten Puffers – des so genannten Projektgesamtpuffers – am Ende des Projekts kompensiert.
Klassisches Projektmanagement (mit möglicher Ressourcenüberlastung)
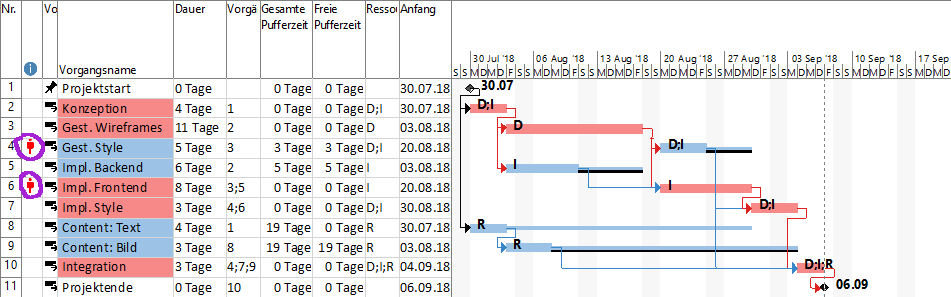
Im klassischen Projektmanagement werden die Vorgänge zusammen mit konservativ geschätzter Dauer, (Ende-Anfang-)Beziehungen und Ressourcen in ein Gantt-Diagramm eingetragen. Dabei kann es allerdings zu Ressourcenüberlastungen kommen. Im Beispiel müsste der Informatiker eine Woche lang gleichzeitig an den Vorgängen 4 und 6 arbeiten. Dies wird in MS Project durch zwei rote Männchen markiert (siehe lila Markierungen).
Klassisches Projektmanagement (mit Kapazitätsausgleich)


Eine Ressourcenüberlastung sollte man durch einen sogenannten Kapazitätsausgleich beheben, da bei Mitarbeitern die Anordnung von Überstunden i. Allg. nur in einem geringen Umfang möglich und sinnvoll ist. Und Maschinen kann man meist auch nur in sehr geringem Umfang unter Überlast laufen lassen.
Wenn der Kapazitätsausgleich termintreu geschehen soll, muss man mehr Ressourcen einplanen. Ein ressourcentreuer Kapazitätsausgleich hat dagegen entweder eine längere Laufzeit oder einen geringeren Funktionsumfang zu Folge. (Beliebt ist auch die Methode, die Qualität zu reduzieren. Aber darauf sollte man besser verzichten.)
Eine einfache, aber wirkungsvolle Methode des ressourcentreuen Kapazitätsausgleichs ist es, zwischen zwei Vorgängen, für die dieselbe Ressource eingesetzt werden muss, eine zusätzliche Ende-Anfang-Beziehung einzuplanen: Die Ressource wird erst zur Erledigung des einen und danach zur Erledigung des anderen Vorgangs eingeplant. In welcher Reihenfolge dies geschieht, ist prinzipiell egal, aber natürlich müssen sachliche Abhängigkeiten berücksichtigt werden. Diese Art des Kapazitätsausgleichs wird i. Allg. als „Resource Leveling“ bezeichnet.
Im gegebenen Beispiel soll der Informatiker die Vorgänge 4, 5 und 6 in folgender Reihenfolge bearbeiten: erst 5, dann 4, schließlich 6 (siehe lila Markierungen). Die Bearbeiungsreihenfolge der Vorgänge 4 und 6 ist nicht vorgegeben, sie kann von anderen Kriterien abhängig gemacht werden. Der Vorgang 5 muss aber auf jeden Fall vor den beiden anderen Vorgängen stattfinden, wie man dem obigen Diagramm unschwer entnehmen kann.
Achtung: Beim Resource Leveling darf die Ende-Anfang-Beziehung 5 → 4 nicht vergessen werden, da anderenfalls im nachfolgenden Diagramm für den Vorgang 5 ein um fünf Tage längerer Puffer ermittelt werden würde. Diesen Puffer gibt es jedoch – wegen der Ressourcenknappheit – nicht: Der Informatiker würde sonst zu spät mit der Arbeit an Vorgang 4 beginnen.
Anmerkung: In vielen Teilen Bayerns ist der 15. August ein Feiertag (Mariä Himmelfahrt), in Augsburg ist überdies der 8. August ein Feiertag (Friedensfest). Dies wurde in den nachfolgenden Gantt-Diagrammen nicht berücksichtigt.
Klassisches Projektmanagement (mit Resource Leveling, ohne redundante Beziehungen)
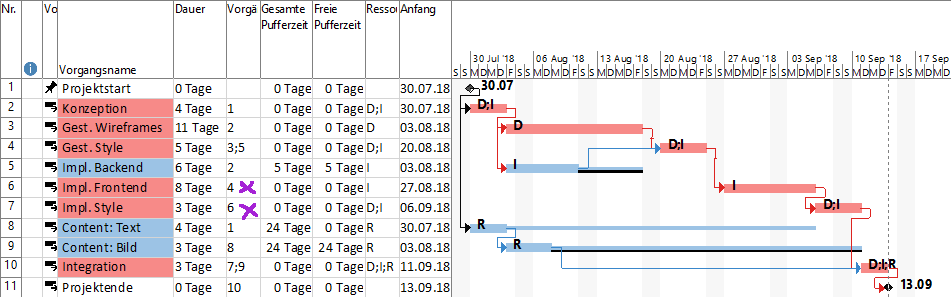
Wenn man ein Gantt-Diagramm per Hand bearbeitet, ist es der Übersichtlichkeit wegen ganz praktisch, nach dem Resource Leveling redundante Ende-Anfang-Beziehungen zu löschen. Beispielsweise kann folgt Vorgang 6 auf Vorgang 4 und damit automatisch auch auf Vorgang 3 und Vorgang 5. Daher braucht man bei Vorgang 6 diese beiden Abhängigkeiten nicht noch einmal zu notieren. Ebenso ist die Erwähnung der Abhängigkeit des Vorgangs 7 vom Vorgang 4 nun redundant und kann ebenfalls entfernt werden.
Allerdings gelten diese Redundanzen nur, solange die Resource-Leveling-Abhängigkeiten gültig sind. Sollte ein zweiter Informatiker diese zusätzlichen Abhängigkeiten überflüssig machen, müssen die ursprünglichen Abhängigkeiten wieder eingetragen werden. Eine genaue Buchführung, welche Abhängigkeit aus welchem Grund existiert, ist in der Praxis unumgänglich.
Critical-Chain-Projektmanagement (mit zu viel Puffer)

Ein erste Unterschied zwischen klassischen Gantt-Diagrammen (CPM) und Gantt-Diagrammen mit kritischer Kette (CCPM) besteht darin, dass der Kapazitätsausgleich mittels Resource Leveling im ersten Fall optional (aber dennoch sehr sinnvoll) ist, im zweiten dagegen zwingend vorausgesetzt wird.
Ein viel wesentlicherer Unterschied ist die Dauer der einzelnen Vorgänge. Anstelle der konservativen Schätzwerte trägt man bei CCPM die Fifty-fifty-Schätzwerte, d. h. die bei der Dreipunkt-Schätzung ermittelten Erwartungswerte ins Gantt-Diagramm ein (siehe lila Markierung – langer Strich).
Die zweifache Summe der zugehörigen Streuungen entspricht in etwa der Summe der Differenzen zwischen den konservativen Schätzungen und den Fifty-fifty-Schätzungen. (Die Abweichung kommt daher, das im Beispiel die konservativen Schätzwerte auf ganze Tage gerundet wurden.)
Die Differenz zwischen den beiden Schätzungen kann man als Projektpuffer ans Projektende einfügen (siehe lila Markierung – kurzer Strich). Damit ändert sich nicht die Gesamtlaufzeit des Projekts, aber dennoch hat man schon etwas gewonnen:
- Das Studentensyndrom und das Parkinsonsche Gesetz („Arbeit dehnt sich in genau dem Maß aus, wie Zeit für ihre Erledigung zur Verfügung steht“) kommen weniger zum Tragen.
- Es wird zwischen einem internen und einem externen Projektende unterschieden (siehe lila Markierungen – Kringel). Der dazwischenliegende Zweitraum dient als Puffer gegen unvorhergesehene Ereignisse.
- Der aktuelle Pufferverbrauch ist in sehr guter Risikoindikator, um frühzeitig Terminprobleme aufzudecken.
| Summe kons. $- μ$ für den kritischen Pfad (rot): |
$1+4+1+3+1+1$ | $= 11 $ | $= 11 $ |
|---|---|---|---|
| 2 * Summe der Streuungen des kritischen Pfads (rot): |
$2(σ_2+σ_3+σ_4+σ_6+σ_7+σ_{10}) $ $= 2(0,4+1,9+0,4+1,4+0,4+0,3) = $ |
$9,6 $ | $\approx 10 $ |
Critical-Chain-Projektmanagement

Schon den Entwicklern von PERT (die erstmals die Dreipunkt-Schätzung propagiert haben) war bekannt, dass man den Zentralen Grenzwertsatz der Statistik anwenden kann, um den Projektgesamtpuffer zu ermitteln. Dieser besagt im Wesentlichen, dass es ausreicht, die Wurzel aus der Summe der Quadrate der Einzelstreuungen zu berechnen und mit einem geeigneten Faktor zu multiplizieren.
Die Wurzel ist im Allgemeinen deutlich kleiner als die Summe der einzelnen Abweichungen. Als Faktor bietet sich 1 oder 2 an. Im ersten Fall beendet man fünf von sechs Projekten fristgerecht, im zweiten sogar 19 von 20. Der erste Fall ist sicherlich riskanter, bietet aber den Vorteil von kürzeren Projektlaufzeiten, was einen Wettbewerbsvorteil darstellen kann.
| Projektgesamtpuffer gemäß Zentralem Grenzwertsatz |
$2\times\sqrt{σ_2^2+σ_3^2+σ_4^2+σ_6^2+σ_7^2+σ_{10}^2} = $ $2\times\sqrt{0,4^2+1,9^2+0,4^2+1,4^2+0,4^2+0,3^2}$ |
$\approx 4,96$ | $\approx 5$ |
|---|---|---|---|
| Zubringerpuffer 1 gemäß Zentralem Grenzwertsatz |
$3\times\sqrt{σ_5^2} = 3\times\sqrt{1,1^2}$ | $=3,3$ | $\approx 3$ |
| Zubringerpuffer 2 gemäß Zentralem Grenzwertsatz |
$3\times\sqrt{σ_8^2+σ_9^2} = 3\times\sqrt{0,4^2+0,4^2}$ | $\approx 1,70$ | $\approx 2$ |
Goldratt geht noch einen Schritt weiter als die PERT-Entwickler. Er fordert auch für nicht-kritische Pfade – die so genannten Zubringerpfade – den jeweiligen Puffer gemäß dem Zentralem Grenzwertsatz zu berechnen. Anschließend wird der Start des Zubringerpfades von Hand (lila Markierungen) soweit nach hinten verschoben, dass dem Zubringer nur noch ein rechnerisch ausreichender Puffer zur Verfügung steht. Eine Vorgangskette so spät wie möglich zu beginnen, biete zwei weitere wesentliche Vorteile:
- Das Studentensyndrom und das Parkinsonsche Gesetz kommen auch hier weniger zum Tragen.
- Änderungen sind für Vorgang, die noch nicht begonnen oder gar beendet wurden wesentlich einfacher vorzunehmen: Eine einfache Planänderung reicht aus.
Durch diese beiden Änderungen hat sich die Projektdauer um 6 Werktage verkürzt und der Start der Content-Erstellung um 13 Werktag nach hinten verschoben.
Anmerkung: Für die Berechnung des Zubringerpuffers kann man ruhig einen etwas größeren Faktor als für die Berechnung des Projektgesamtpuffers verwenden. Hier besteht keine Konkurrenzsituation zu anderen Unternehmen und Mitarbeiter, die an nicht-kritischen Vorgängen arbeiten, werden häufiger mal in ihrer Tätigkeit unterbrochen (zumindest wen das Management dafür Sorge trägt, dass Mitarbeiter, die an zeitkritischen Vorgängen arbeiten, möglichst von anderen Tätigkeiten entlastet werden).
Quellen
- Goldratt (2002): Eliyahu M. Goldratt; Die kritische Kette − Ein Roman über das neue Konzept im Projektmanagement; Verlag: Campus Verlag; ISBN: 3593370913; 2002; Quellengüte: 5 (Buch)
- Leach (2005): Lawrence P. Leach; Critical Chain Project Managgement; Auflage: 2; Verlag: Artech House; ISBN: 1580539033; 2005; Quellengüte: 5 (Buch)
- Uwe Techt, Das aktuelle Stichwort: „Critical-Chain-Projektmanagement“, April 2005 (projektMANAGEMENT aktuell 2/05)
- Uwe Techt und Holger Lörz, Projektmanagement: Mit der Critical-Chain-Methode die Projektlaufzeit entscheidend verkürzen, Januar 2005
- Oliver Steeger, Projektmanagement: Die kritische Kette treibt Projekte an, Mai 2005
- Mike Mannion and Sven Ehrke, Introduction to Critical Chain, TOC Update, Februar 2006